O vértice da parábola - uma outra abordagem

Se considerarmos uma função quadrática real genérica f(x) = ax² + bx + c, existem algumas formas distintas de obter as coordenadas do vértice da parábola que é o gráfico desta função.
Ora, o vértice da parábola é o único ponto de intersecção de uma parábola com uma certa recta horizontal de equação y = k.
Com isto em mente, vamos determinar o valor de k e as coordenadas do vértice.
Sendo o vértice o único ponto comum a essa recta e a essa parábola, as suas coordenadas são as soluções do sistema:

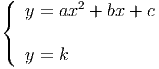
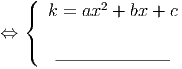
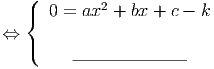
Ora, para que a solução seja única temos de ter

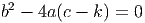
E portanto a coordenada x será:

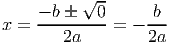
E, a coordenada y terá o valor de k, pois o vértice pertence à recta y = k.
Assim sendo basta-nos recorrer à equação

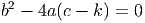
e resolver.

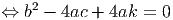
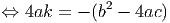
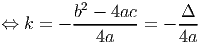
E, então as coordenadas do vértice são:

A propósito de funções quadráticas, sugiro uma visita à primeira blog-app deste blog, que calcula entre outras coisas o vértice e os zeros de uma função quadrática.
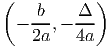
Para os que têm uma calculadora gráfica programável: sim também dá para "meter" na calculadora...
Bons estudos