
Explicações de Matemática
por Carlos Paulo A. Freitas
segunda-feira, 31 de março de 2014
http://cpaulof2.blogspot.pt/2014/03/a-area-e-o-perimetro-de-poligonos.html
Passar com negativa no ensino secundário
Tendo em conta que na avaliação entram outros factores para além do conhecimento/notas dos exames, o cenário é aterrador pois significa que os alunos transitam com um grande défice de conhecimento.
Este ano, não foi excepção, e mais uma vez assisto ás contas desesperadas de quem passou com nota abaixo de 10 (e só me procurou a meio do ano lectivo... explicações de Matemática levam algum tempo a sortir efeito, quando se trata de falta de bases ou de maus hábitos de trabalho)
Quando em explicações peço a estes alunos para lutarem desde princípio para o 20, pensam que estou a gozar. Não estou! É um assunto demasiado sério. E realisticamente, duvido que atinjam o 20, mas é a luta.
a sério que faz os os resultados aparecerem..
Ora, as explicações existem para colmatar falhas e corrigir hábitos nos alunos,e com uma luta destas podemos detectar muito do que está mal..
Mas estes alunos têm mesmo de trabalhar.
(Já agora... sim já uma vez consegui que um destes alunos tivesse um 20.. até hoje acho que ele próprio está incrédulo)
Estas más notas acabam por gerar uma falta de confiança, que mesmo com explicações é complicado inverter.
Já tive vários casos de sucesso a inverter esta mentalidade, a que se seguiram notas razoáveis nos testes e alguns insucessos mas com melhoria significativa nos testes.
Sem trabalho não há resultados, e sem confiança... o trabalho não rende.
Em Matemática, pela sua especificidade, o trabalho é fundamental, e uma confiança muito abalada não ajuda em nada (e aqui posso falar por exemplo, do meu último mestrado onde havia uma peça...).
Eu acabo por insistir, por vezes tornando-me chato..., mas tento sempre fornecer material que seja interessante (gostam das ninhas blog-apps? São apenas 1% do material que uso...)...
Tenho imensa pena de ver alunos desistir de Matemática por acharem que não são capazes...
Alunos a quem não falta inteligência, mas falta motivação e trabalho.
Há alunos que simplesmente se recusam a trabalhar para ultrapassar as suas dificuldades.
Outras vezes, tenho de reconhecer que por vezes o maior motivo da falta de confiança reside no professor (mas alto lá... acusar um professor, não é algo que eu faça de ânimo leve. até porque a maioria dos profissionais que eu conheço, e de onde vêm muitos alunos para as minhas explicações são excelentes e dedicados profissionais, portanto, antes de acusar um professor, procure exaustivamente todas as causas possíveis...)
Por outro lado, existem aqueles alunos que apanham tudo á primeira, e para quem tudo é facil... Mas atenção, pode haver sempre uma altura em que as coisas não sejam assim, e portanto, a falta de trabalho pode levar a um descarrilamento total, que é o que acontece muitas vezes, quando há uma mudança. Ou de professor, ou de escola, ou de turma...
Permitir passar com negativa é dar uma carta de confiança a um aluno, mas o que tenho visto... é desesperante. Alguém tem de convencer estes alunos que só com trabalho se ultrapassam as dificuldades, de preferência sem os traumatizar...
Permitir passar com negativa pode ter sido uma boa intenção... mas para muita gente, essa opção é muito discutível, visto que acaba por complicar também as contas de acesso ao ensino superior..
Compreendo que nem todos possam gostar de Matemática... mas tem sido desesperante ver alunos e mesmo ex-alunos em situações bem complicadas, alunos que por mais que eu queira ajudar, não consigo fazer milagres... :( e por vezes... tenho mesmo de recusar dando a triste notícia de que já nada se pode fazer.
sexta-feira, 28 de março de 2014
O fantastico e
Limites notáveis: e
Um dias destes tenho de lhe dar uma sequela.
E, já agora, a resolução ao exercício proposto é:
Ou, alternativamente, para escrever menos...
segunda-feira, 24 de março de 2014
ver secção Blog Apps.
Geogebra: Rotações 001
Penso que esta applet será particularmente útil para alguns alunos de 6º ano.
sábado, 22 de março de 2014
O teste intermédio de 9º ano (2013/2014)
Critérios de classificação
Daqui a uns dias actualizo o pdf com testes intermédios, disponível no separador arquivos
quinta-feira, 20 de março de 2014
Rumo à anarquia: os alunos que não querem aprender nem deixam os outros aprender
http://dererummundi.blogspot.pt/2014/03/o-colapso-da-escola.html
A situação não é nova... há mais de duas décadas, quando eu estava no 7º ano estava numa turma onde as diferenças de idades tinham valores anormalmente grandes. Tinha eu 11 anos e tinha um colega de 16 que usava os mais novos como alvos das suas patifarias... "bullying" como se diz hoje em dia.
Lembro-me que nas aulas de ciências e mesmo Matemática, era complicado aprender alguma coisa pois o idiota não deixava uma pessoa concentrar-se.
Era tão mau que lembro-me como se fosse hoje..
Fazer queixa dele era sinónimo de arranjar problemas nos intervalos. Lembro-me uma vez de ter tido uma luva de cabedal a tapar-me o nariz e a boca...e estar prestes a perder os sentidos e de ser salvo pelos contínuos.
Nem vou falar das aulas de educação física!
Lembro-me de fazer queixa à directora de turma, e de nada me valer, de ter sido a minha mãe apresentar a situação e a professora a dizer que não sabia de nada...
(Mas, vendo bem, o que esperar de uma professora de inglês que me corrigiu quando eu disse que o Astérix era gaulês? Para ela Astérix era galês, do país de Gales)
Felizmente no 8º ano, essas pessas já não estavam na turma.... Foram substituidas por outras de igual qualidade, mas de idades mais perto da minha... O problema não era (só) a idade! Mas no 9º, depois de 2 anos a pedir para ser colocado numa turma da parte da manhã, o meu pedido foi finalmente atendido, e tive um dos anos mais calmos e mais proveitosos.
Mesmo sem tentar esquecer as "faltas colectivas" de castigo que nos marcava o professor de Matemática que não controlava os alunos...
De notar que mesmo naquelas condições, em cada ano lectivo acabei sempre com a nota máxima em Matemática...
Quantos potenciais bons alunos não estarão a ser estragados por situações deste tipo?
Nas explicações eu tenho armas que não existem na escola:
Posso expulsar um aluno por mau comportamento ou por se recusar a trabalhar.
Aliás, explicações não funcionam com alunos nestas condições: Perturbam quem quer e precisa delas!
Não se pense que são necessários grupos grandes para isto! Os meus grupos são bem pequenos e, principalmente nos 2ºs e 3º ciclo aparece sempre alguém que está mais interessado em perturbar do que em estudar.
Mesmo com um só aluno, por vezes acontece!
Por mais interessante que seja o assunto ou a forma como está a ser ensinado ou explicado.
Nesses dias mais vale o explicando/aluno ficar em casa...
"Se não te apetece trabalhar, porque é que não ficas em casa?"
"Porque o meu pai/minha mãe não quer.".
Ok, e o que é que eu tenho a ver com isso? Vou pagar eu e os outros explicandos com as nossas paciências?
Não! Contrariamente à escola, explicações não são obrigatórias. Aliás, pela própria definição de explicações, os alunos deviam ser voluntários, portanto, eu posso e dispenso mesmo explicandos desinteressados, sempre de forma justificada..
Por vezes até se nota que o explicando veio de uma sala onde o único interessado em trabalhar foi o professor.
Não me venham condenar o professor pela falta de educação dos filhos...
O professor não tem grandes ferramentas disciplinares, e sinceramente, "dar sermões" ou gritar com os alunos nada resolve e até pode ter uma capacidade detrimental na capacidade de aprendizagem nessa aula.
Em caso de explicações, se não quer ou não está interessado, fique em casa... volte quando e se quiser, e fundamentalmente não negue o direito a quem quer!
E certamente, tendo eu uma lista de espera de alunos em explicações, não sou eu que vou ter problemas em explulsar quem não está interessado...
Pena que os professores nem sempre tenham as armas que eu tenho...
Se é um dos meus explicandos: Sim... eu "dispenso" pessoas.
sexta-feira, 14 de março de 2014
Dia do Pi
Para comemorar o dia, dei aos meus explicandos de 6º ano a versão 1.00 desta ficha
quinta-feira, 13 de março de 2014
O vértice da parábola - uma outra abordagem
Se considerarmos uma função quadrática real genérica f(x) = ax2 + bx + c,
existem algumas formas distintas de obter as coordenadas do vértice da parábola
que é o gráfico desta função.
Ora, o vértice da parábola é o único ponto de intersecção de uma parábola com
uma certa recta horizontal de equação y = k.
Com isto em mente, vamos determinar o valor de k e as coordenadas do
vértice.
Sendo o vértice o único ponto comum a essa recta e a essa parábola, as suas
coordenadas são as soluções do sistema:
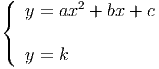
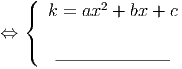
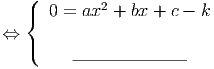
Ora, para que a solução seja única temos de ter
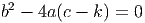
E portanto a coordenada x será:
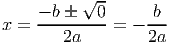
E, a coordenada y terá o valor de k, pois o vértice pertence à recta y = k.
Assim sendo basta-nos recorrer à equação
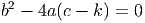
e resolver.
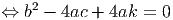
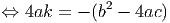
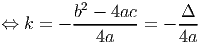
E, então as coordenadas do vértice são:
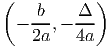
Para os que têm uma calculadora gráfica programável: sim também dá para "meter" na calculadora...
Bons estudos
quarta-feira, 12 de março de 2014
Testes intermédios de Matemática A - 11º ano (2006-2014)
Actualizei-o há pouco...
A versão mais recente é a versão 4 de 2014
(Adicionei o teste de ontem)
Adicionei também as resoluções de todas as versões 1 de todos os testes intermédios de Matemática A 11º, disponibilizadas pelo GAVE/IAVE neste ficheiro.
segunda-feira, 10 de março de 2014
Blog-Apps: Função Quadrática
Na versão actual apenas calcula as coordenadas do vértice do gráfico de uma função quadrática (como se sabe, o gráfico é uma parábola).
Ainda não está pronta, mas já funciona pois depende de um script que foi adaptado de uma das minhas cpcalculadoras javascript, e que continua a ser modificado para servir para uma nova versão da CpcalculadoraJS e para ser utilizável em várias Blog-Apps Matemáticas que tenciono partilhar neste blog.
Nesse (java)script estão a ser adaptados e criados novos objectos para se tornar mais fácil utilizar e apresentar fracções, radicais e outros objectos algébricos.
É um trabalho que leva o seu tempo, e depende da minha disponibilidade para programar...
Algumas destas blog-apps são facilmente implementáveis nas calculadoras gráficas programáveis que estão disponíveis para os alunos do nosso ensino secundário.
domingo, 2 de março de 2014
Testes intermédios de Matemática A - 11º ano (2006-2013)
Actualizei-o há pouco...
A versão mais recente é a versão 2 de 2014
(havia um erro no índice nas duas versões anteriores)
Adicionei também as resoluções de todas as versões 1 de todos os testes intermédios de Matemática A 11º, disponibilizadas pelo GAVE neste ficheiro.


